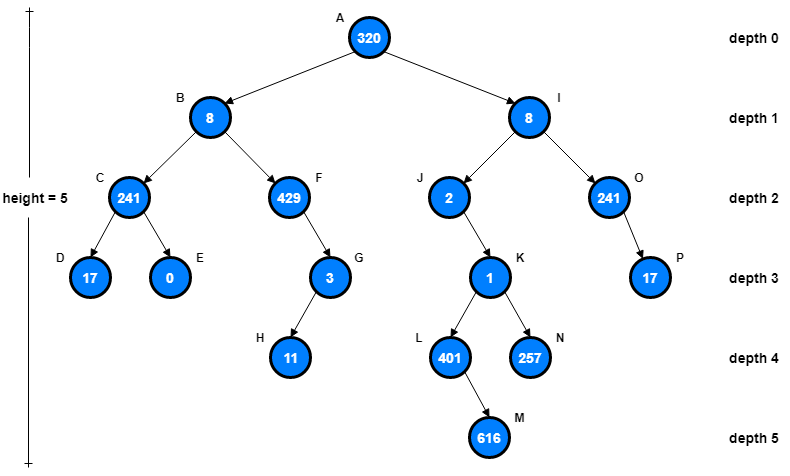
Generic Tree

is to create another array and store sum from start to i at the ith index in this array. The sum of a given range can now be calculated in $O(1)$ time, but update operation takes $O(n)$ time now. This works well if the number of query operations is large and very few updates. What if the number of queries and updates are equal? It is a hierarchical structure as elements in a Tree are arranged in multiple levels. In the Tree data structure, the topmost node is known as a root node. Each node contains some data, and data can be of any type.

Tree

Terms:

TREES - Learn with Data Structures

Code to implement [src code]

class Node:
    def __init__(self, val, children=None):
        self.val = val
        self.children = children

Traversal

def preorder(root):
    if root:
        print(root.val)
        for child in root.children:
            preorder(child)

def postorder(root):
    if root:
        for child in root.children:
            postorder(child)
        print(root.val)

Binary Tree

Binary Tree - emre.me

Code to implement [src code]

class Node:
    def __init__(self, val, lch=None, rch=None):
        self.val = val
        self.lch = lch
        self.rch = rch

Traversal

def preorder(root):
    if root:
        print(root.val)
        preorder(root.lch)
        preorder(root.rch)

def postorder(root):
    if root:
        postorder(root.lch)
        postorder(root.rch)
        print(root.val)

Linear Structure Maintained by Tree

Binary Indexed Tree

Let us consider the following problem to understand Binary Indexed Tree. We have an array arr[0 ... n-1]. We would like to

1. Compute the sum of the first i elements.

2. Modify the value of a specified element of the array arr[i] = x where 0 <= i <= n-1.

A simple solution is to run a loop from 0 to i-1 and calculate the sum of the elements. To update a value, simply do arr[i] = x. The first operation takes $O(n)$ time and the second operation takes $O(1)$ time. Another simple solution is to create an extra array and store the sum of the first i-th elements at the i-th index in this new array. The sum of a given range can now be calculated in $O(1)$ time, but the update operation takes $O(n)$ time now. This works well if there are a large number of query operations but a very few number of update operations.

Could we perform both the query and update operations in $O(\log n)$ time?

Take a look at this example.

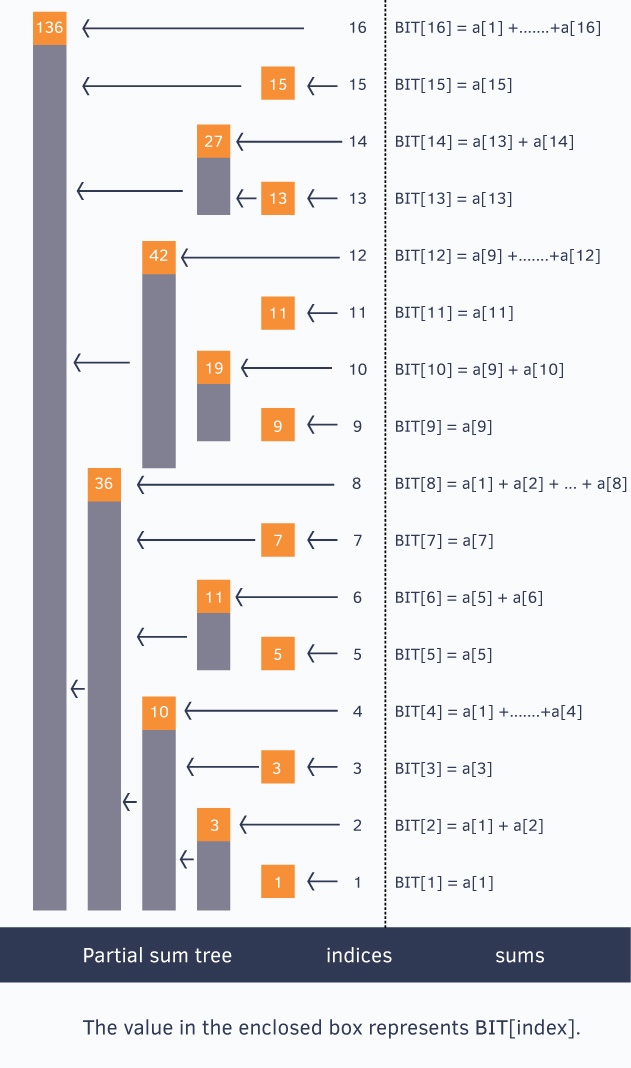
Each Orange node maintains an interval sum of numbers. If we rotate it, we can have a better understanding.

For example, to get the interval sum(or any other data of an interval you defined) of [0, 10]. just add 2 values rather than 11 values. Try to find which 2 values are components to sum up.

Segment Tree

Let us consider the previous question in Binary Indexed Tree

A simple solution is to run a loop from l to r and calculate the sum of elements in the given range. To update a value, simply do arr[i] = x. The first operation takes $O(n)$ time and the second operation takes $O(1)$ time.

Another solution how does it work? we perform both the operations in $O(\log N)$ time once given the array? We can use a Segment Tree to do both operations in $O(\log N)$ time.

1. Leaf Nodes are the elements of the input array.

2. Each internal node represents some merging of the leaf nodes. The merging may be different for different problems. For this problem, merging is the sum of leaves under a node.

An array representation of a tree is used to represent Segment Trees. For each node at index i, the left child is at index 2 * i + 1, the right child at 2 * i + 2 and the parent is at ⌊(i – 1) / 2⌋(Note: ⌊expression⌋notation means flooring).