Breadth First Search
In the last section you have learned one of the Algorithms to solve the Shortest Path problem. Before I introduced the following Dijkstra and SPFA Algorithms, it is needed to have some ideas on Breadth First Search which is widely applied on many kind of searching problems as well as the following two Shortest Path finding Algorithms.
You may noticed that the name of Breadth First Search (abbr. BFS) is similar to the name of DFS. The implementation of the two algorithms is wholey different since DFS adopts recursion while BFS adopts methodology of queue (remember that it is a data structure introduced below?).
A lively metaphor is that BFS is like flooding (or spread of epidemic) , you can check this Youtube video to see the algorithm animation.
We can see that, for nodes in same depth, they are visited at the same time (actually, it have the order, but the node in next depth cannot be visited the same time as current depth).
Here shows the pseudo code.
queue = []
queue.append(start)
visit(start)
while queue not empty:
this_node = queue.pop()
# do some stuffs
for next_node in this_node.childrens:
if next_node not visited:
queue.append(next_node)
visit(next_node)visit() is the function to mark a node as visited this_node.childrens means the adjacent node to current node
Maze Problem II
Adopting BFS in solving Maze Problem is another way of thinking. For the question, please refer to the previous Maze Problem I. Let us try to implement the maze solver by adopting BFS.
Maze parser code here: (You are free to change the map pattern if you like using maze.py)
Sol.
LC 733
An image is represented by an m x n integer grid image where image[i][j] represents the pixel value of the image.
You are also given three integers sr, sc, and newColor. You should perform a flood fill on the image starting from the pixel image[sr][sc].
To perform a flood fill, consider the starting pixel, plus any pixels connected 4-directionally to the starting pixel of the same color as the starting pixel, plus any pixels connected 4-directionally to those pixels (also with the same color), and so on. Replace the color of all of the aforementioned pixels with newColor.
Return the modified image after performing the flood fill.
Example 1:
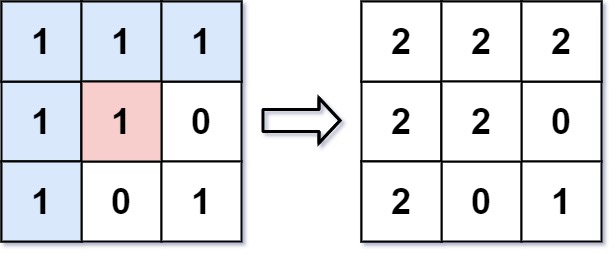
Example 2:
Constraints:
m == image.lengthn == image[i].length1 <= m, n <= 500 <= image[i][j], newColor < 2160 <= sr < m0 <= sc < n
LC 1559
Given a 2D array of characters grid of size m x n, you need to find if there exists any cycle consisting of the same value in grid.
A cycle is a path of length 4 or more in the grid that starts and ends at the same cell. From a given cell, you can move to one of the cells adjacent to it - in one of the four directions (up, down, left, or right), if it has the same value of the current cell.
Also, you cannot move to the cell that you visited in your last move. For example, the cycle (1, 1) -> (1, 2) -> (1, 1) is invalid because from (1, 2) we visited (1, 1) which was the last visited cell.
Return true if any cycle of the same value exists in grid, otherwise, return false.
Example 1:
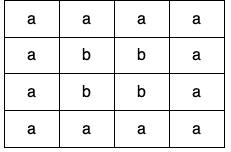
Example 2:
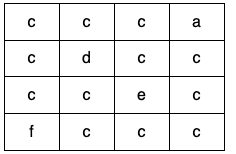
Example 3:
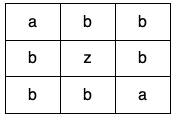
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 500gridconsists only of lowercase English letters.
Last updated
